In this post first we talk about the importance of maximum likelihood and then we evaluate the Expectation Maximization (EM) algorithm.

Maximum Likelihood Interpretation:

Suppose that we have a dataset of i.i.d samples $\{x_i\}_{i=1}^{N_D}$ in which $N_D$ is the number of datapoints. We are assuming each datapoint was independently sampled from $p(x;\boldsymbol\theta)$ and we want to estimate $\boldsymbol\theta$. Since these samples are i.i.d we can factorize their joint probability:

$$p(x_1,x_2,\ldots,x_{N_D};\boldsymbol\theta) = \prod_{i=1}^{N_D} {p(x_i;\boldsymbol{\theta})}$$

Maximum likelihood method looks for the parameter that maximizes this joint probability (or the log of joint probability):

$$\hat{\boldsymbol\theta}=\arg\max_{\boldsymbol\theta} \sum_{i=1}^{N_D}{\log p(x_i;\boldsymbol\theta)}$$

Now suppose that $y=\{y_k\}_{k=1}^{K}$ is the set of unique datapoints and $N_{D}=\sum_{k=1}^{K}{N_k}$, so we can rewrite the equation for $\hat{\boldsymbol\theta}$:

$$\begin{align} \hat{\boldsymbol\theta}&= \arg\max_{\boldsymbol\theta} \sum_{k=1}^{K}{N_k\log p(y_k;\boldsymbol\theta)}\\ &=\arg\max_{\boldsymbol\theta} \sum_{k=1}^{K}{\dfrac{N_k}{N_D}\log p(y_k;\boldsymbol\theta)}\\ \end{align}$$

In this equation $\dfrac{N_k}{N_D}$ is the frequency of each datapoint which shows the emprical distribution of unique datapoints, so by defining $q(y_k)$ as our emprical distribution:

$$\begin{align} \hat{\boldsymbol\theta} &=\arg\max_{\boldsymbol\theta} \sum_{k=1}^{K}{q(y_k)\log p(y_k;\boldsymbol\theta)}\\ &=\arg\max_{\boldsymbol\theta} \sum_{k=1}^{K}{q(y_k)\log \dfrac{p(y_k;\boldsymbol\theta)}{q(y_k)}}\\ &=\arg\max_{\boldsymbol\theta} D_{\mathrm{KL}}\big(q(y)\|p(y;\theta)\big) \end{align}$$

The last equation shows that by using maximum likelihood we are minimizing the KL-divergence between emprical distribution ($q(y)$) and the predefined model ($p(y;\theta)$).

Expectation Maximization:

Sometimes it’s not easy to find $\hat{\boldsymbol{\theta}}$ directly, but adding a latent variable to the model makes the joint probability of $p(\boldsymbol{X},\mathbf{z};\boldsymbol{\theta})$ easier to deal with. In this part we see how we can find an iterative algorithm to improve approximated parameters in each step. We know that for a concave function if $\lambda_1\geq 0,\ldots,\lambda_n\geq 0$ and $\sum_{i} \lambda_i =1$ we have Jensen’s inequality. $f\big(\sum_i \lambda_i x_i\big) \geq \sum_i \lambda_i f(x_i)$

Image below depicts this inequality for a simple case that we have just two points ($n=2$):

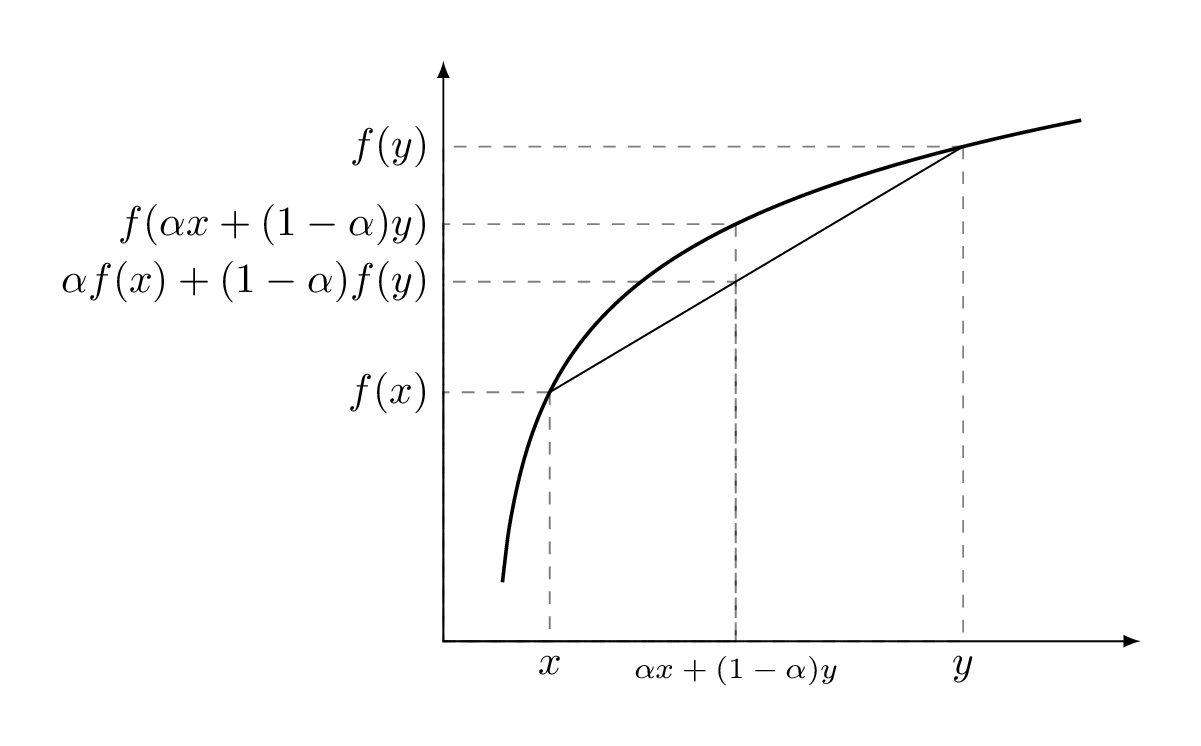
In statistics a special case of Jensen’s inequality holds for the expected value of a concave function.

$$\begin{align} \mathbb{E}[f(x)]&=\sum p(x)f(x)\\ &\leq f\big(\sum xp(x)\big)\\ &=f\big(\mathbb{E}[x]\big) \end{align}$$

Now suppose that $\mathbf{X}$ is the set of all datapoints and in $n^{\mathrm{th}}$ iteration the estimate for $\theta$ is $\theta_n$. We want to maximize $L(\boldsymbol\theta)$:

$$L(\boldsymbol\theta)=\log p(\mathbf{X};\boldsymbol\theta)$$

Since we want to make sure that in each iteration our likelihood is getting better ($L(\boldsymbol\theta_{n+1})\geq L(\boldsymbol\theta_{n}))$, our best action would be finding the parameter $\boldsymbol{\hat{\theta}}$ that maximizes the distance between $L(\boldsymbol\theta)$ and $L(\boldsymbol\theta_n)$:

$$\Delta(\boldsymbol\theta|\boldsymbol\theta_n)= L(\boldsymbol\theta)- L(\boldsymbol\theta_n)= \log \bigg(\dfrac{p(\mathbf{X};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n) } \bigg)$$

We know that $\log$ function is concave and adding a sum inside the $\log$ would provide this opportunity to use Jensen’s inequality. The numerator of the fraction inside log is a marginal probability that can be written as summation of joint probability:

$$p(\mathbf{X};\boldsymbol\theta)= \sum_\mathbf{z}{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)}$$

And we have:

$$\Delta(\boldsymbol\theta|\boldsymbol\theta_n)= \log \bigg(\sum_{\mathbf{z}}\dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n) } \bigg)$$

Now we see that $\dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n) }$ is playing the role of $f(\mathbf{z})$ and since the summation is over $\mathbf{z}$, we should add a probability distribution of $\mathbf{z}$ (something like $p(\mathbf{z})$) to be able to use Jensen’s inequality. Our different options are:

1- Our first option is $p(\mathbf{z};\boldsymbol\theta_n)$:

$$\begin{align} \Delta(\boldsymbol\theta|\boldsymbol\theta_n) &=\log \bigg(\sum_{\mathbf{z}}p(\mathbf{z};\boldsymbol\theta_n) \dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n)p(\mathbf{z};\boldsymbol\theta_n) } \bigg)\\ &\geq \sum_{\mathbf{z}}p(\mathbf{z};\boldsymbol\theta_n) \log \bigg( \dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n)p(\mathbf{z};\boldsymbol\theta_n) } \bigg) \end{align}$$

So we have found a lower bound for $\Delta(\boldsymbol\theta|\boldsymbol\theta_n)$ and by maximizing this lower bound in each iteration we want to make sure that liklihood is getting better and better:

$$\begin{align} \boldsymbol{\theta}_{n+1}&= \arg\max_{\theta} \sum_{\mathbf{z}}p(\mathbf{z};\boldsymbol\theta_n) \log \bigg( \dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n)p(\mathbf{z};\boldsymbol\theta_n) } \bigg) \\ &= \arg\max_{\theta} \sum_{\mathbf{z}}p(\mathbf{z};\boldsymbol\theta_n) \log { p(\mathbf{X},\mathbf{z};\boldsymbol\theta) } \end{align}$$

But $\boldsymbol\theta_n$ is supposed to include all the parameters needed for the joint probability of $\boldsymbol{X}$ and $\mathbf{z}$ which is $p(\mathbf{X},\mathbf{z};\boldsymbol{\theta_n})$ and in general case $p(\mathbf{z};\boldsymbol\theta_n)$ is just using a subset of parameters defined in $\boldsymbol{\theta_n}$ and some other parameters such as parameters needed for $p(\boldsymbol{X}|\mathbf{z})$ may not be updated. So we can evaluate another option.

2- The second option is $p(\mathbf{z}|\mathbf{X};\boldsymbol{\theta_n})$ that uses all the parameters defined in $\boldsymbol{\theta_n}$:

$$\begin{align} \boldsymbol{\theta}_{n+1}&= \arg\max_{\theta} \sum_{\mathbf{z}}p(\mathbf{z}|\mathbf{X};\boldsymbol{\theta_n}) \log \bigg( \dfrac{p(\mathbf{X},\mathbf{z};\boldsymbol\theta)} { p(\mathbf{X};\boldsymbol\theta_n) p(\mathbf{z}|\mathbf{X};\boldsymbol{\theta_n}) } \bigg) \\ &= \arg\max_{\theta} \sum_{\mathbf{z}} p(\mathbf{z}|\mathbf{X};\boldsymbol{\theta_n}) \log { p(\mathbf{X},\mathbf{z};\boldsymbol\theta) } \end{align}$$

And this last equation is the general form of EM algorithm:

E-step:

Compute the expected value of joint probability:

$$f(\boldsymbol\theta)= \mathbb{E}_{p(\mathbf{z}|\mathbf{X};\boldsymbol{\theta_n})} \bigg[ \log { p(\mathbf{X},\mathbf{z};\boldsymbol\theta) } \bigg]$$

M-step:

Maximize $f(\boldsymbol\theta)$ with respect to $\boldsymbol\theta$:

$$\boldsymbol{\theta}_{n+1}= \arg\max_{\boldsymbol\theta} f(\boldsymbol\theta)$$

Refrences:

1-Maximum Likelihood Estimation

2-The Expectation Maximization Algorithm A short tutorial