Rejection Sampling

Rejection sampling is a simple algorithm to sample from an arbitrary distribution that is hard to sample from directly. The idea is to accept and reject the samples from another distribution which is easy to sample from. Suppose that:

1- $f(x)$ is the target distribution that can be any arbitrary function of $x$, such that:

• $\forall x:\, f(x)\geq 0$ and $\int_{x}{f(x)\, \mathrm{d}x =1}$

2- $g(x)$ is another distribution which is easy to sample from and also for all values of $x$, there exists a constant $M$ satisfying $f(x)\leq M g(x)$.

3- $U$ is the uniform distribution such that:

$$\begin{equation} p(U=u)= \begin{cases} 1 ,& \text{if } 0\leq u\leq 1\\ 0, & \text{otherwise} \end{cases} \end{equation}$$

Now suppose that we have one sample generator for distribution $g$ (which was easy to do the sampling ) and one for the uniform distribution $U$.

In each step, first we generate a sample from the $g$ distribution and we call it $y$, also we get another sample from the uniform distribution and we call it $u$. Now if $u < \dfrac{f(y)}{Mg(y)}$ we accept this sample and otherwise it should be rejected.

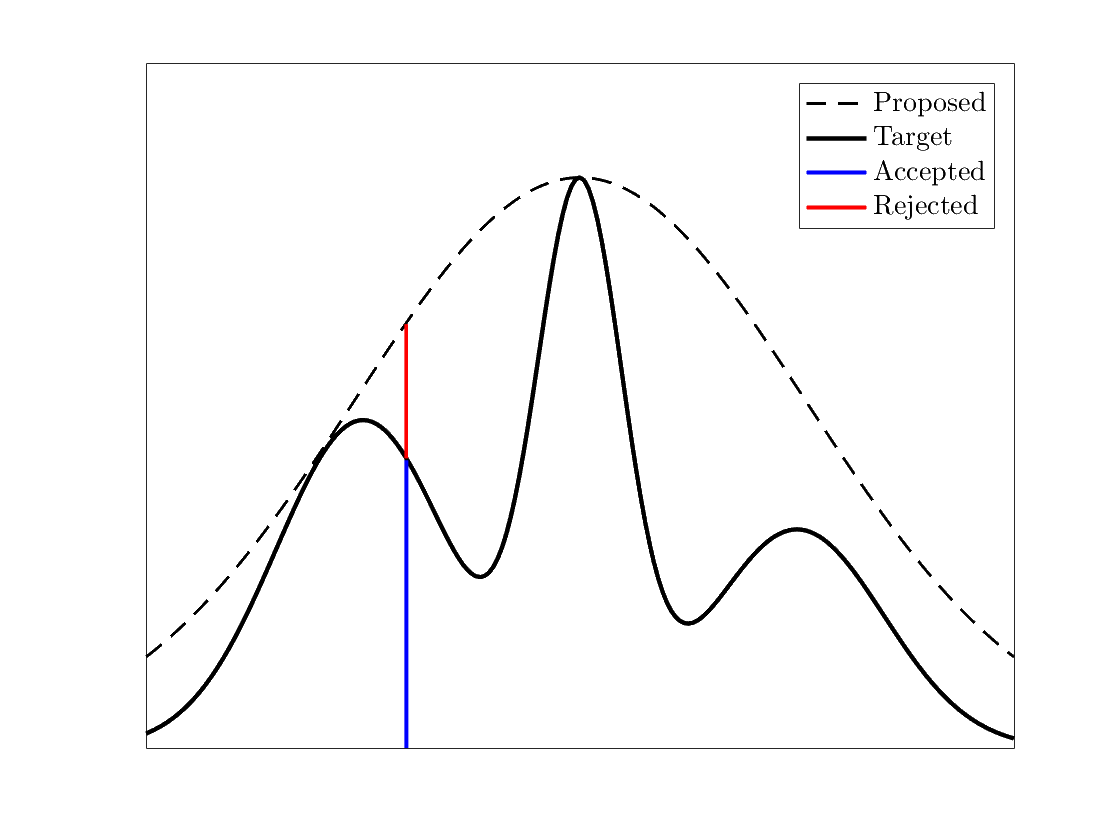
We want to show that by continuing this algorithm the emprical distribution for the accepted samples is equal to the desired $f(x)$ distribution.

First it’s obvious that we are looking for $p_{\mathrm{emprical}}{(y)}$ which is equal to $p(y|\mathrm{accept})$. By using Bayes rule we have:

$$\begin{equation} p(y|\mathrm{accept}) = \dfrac{ p(\mathrm{accept}|y) p(y) }{ p(\mathrm{accept}) } \end{equation}$$

Now we can evaluate each term separately.

1- $p(\mathrm{accept}|y)$ is the probability that the sample is accepted which is equal to $p\big(u < \dfrac{f(y)}{Mg(y)}\big) = \dfrac{f(y)}{Mg(y)}$

2- $p(y)$ is the distribution used for generating $y$, so we have $p(y)= g(y)$

3- $p(\mathrm{accept})=\int p(\mathrm{accept}|y)p(y) \mathrm{d}y=\int \dfrac{f(y)}{M} \,\mathrm{d}y= \dfrac{1}{M}$

And the proof is complete:

$$p(y|\mathrm{accept})=\dfrac{ \dfrac{f(y)}{Mg(y)} g(y) }{\dfrac{1}{M}}= f(y)$$