In probabilistic machine learning we are always assuming that our observations $\{x_1,x_2,\ldots,x_N\}$ are samples generated from probability distributions and we are dealing with their joint probability:

$$\begin{equation} p(x[0],x[1],\ldots,x[N-1];\theta) \end{equation}$$

For each particular problem (or dataset) we can define our model for this joint probability. when the notation used for the probability distribution has semicolon (i.e. $p(x;\theta)$), it means that in our predefined model we have a deterministic but unknwon parameter $\theta$ and we are looking for an estimator (a function of samples) to approximate this parameter :

$$\hat{\theta}=g(x[0],x[1],\ldots,x[N-1])$$

For example in language modeling we can assume words in a sentence are i.i.d data samples (the sentence is an array of these words $s=\{w[0],w[1],\ldots,w[N-1] \}$) and our aim is to find the parameters of their distribution:

$$w[i]\sim p(w;\theta)$$

We can improve this model by adding latent variables. In language modeling we know that sentences are generated by grammar rules, so this prior information can help us to make more accurate models. In other words, in this new model first there are samples generated from hidden variables ($\mathbf{z}$) and then our observations ($\mathbf{x}$) are generated by them.

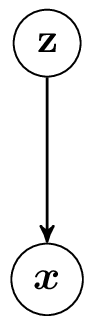
After introducing the latent variables to our model instead of the joint probability of datasamples we should define the joint probability of data and the hidden variables in $p_{\boldsymbol{\theta}}(\mathbf{x},\mathbf{z})$.

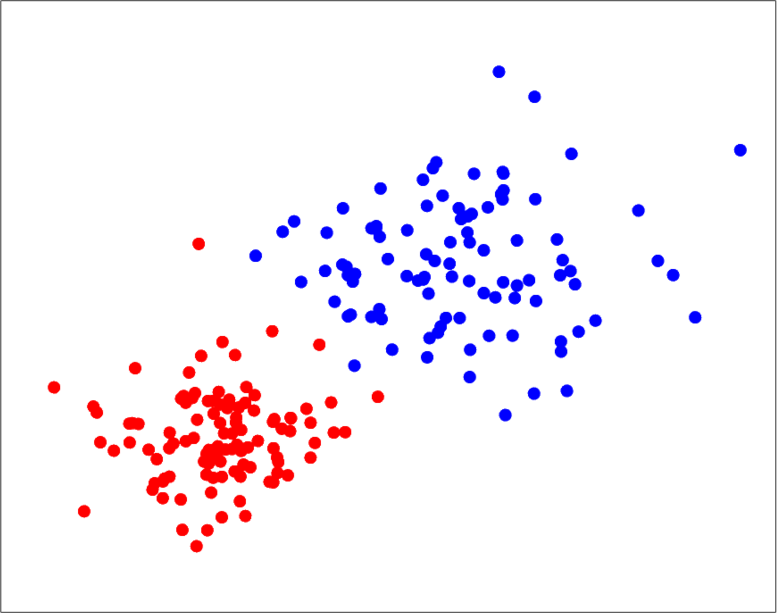
A good example for adding latent variables is clustering. Suppose that first we just see the raw datapoints:

After observing the data we can decide to have two clusters in our model and simply define $p_{\boldsymbol{\theta}}(\mathbf{x}|z=0) = \mathcal{N}(\mu_0,\sigma_0)$ and similarly $p_{\boldsymbol{\theta}}(\mathbf{x}|z=1) = \mathcal{N}(\mu_1,\sigma_1)$ . Also we should define the prior information for $p_{\boldsymbol\theta}(\mathbf{z})$. (We sometimes assume that the prior for $\mathbf{z}$ lacks any unknown parameter such as $\mathcal{N}(0,1)$). So in this clustering example our model for the conditional probability is Gaussian and the parameters for them are $\boldsymbol{\theta}=\{\mu_0,\sigma_0,\mu_1,\sigma_1\}$.

Now since $\mathbf{z}$ is not deterministic and it was defined to be a random variable, after observing the data we want to infer $p(\mathbf{z}|\mathbf{x})$ and we call it the posterior. By using Bayes rule we can define this distribution based on the model we defined:

$$p(\mathbf{z}|\mathbf{x})=\dfrac{p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z})}{p_{\boldsymbol\theta}(\mathbf{x})}$$

Also we know that in continuous case:

$$\begin{equation} p_{\boldsymbol\theta}(\mathbf{x})=\int p_{\boldsymbol\theta}(\mathbf{x}|\mathbf{z}) p_{\boldsymbol\theta}(\mathbf{z}) \, \mathrm{d}\mathbf{z} \end{equation}$$

Since this integral is over all possible values for $\mathbf{z}$ if the dimension of $\mathbf{z}$ is high or the number of different possible values it can take is infinite then $p(\mathbf{z}|\mathbf{x})$ is intractable. Now one of the solutions would be estimating $p(\mathbf{z}|\mathbf{x})$ by defining a tractable distribution ( a simple distribution that we define ourselves) such as $q_{\mathbf{\phi}}(\mathbf{z})$ and minimizing the divergence between $q_{\boldsymbol{\phi}}(\mathbf{z})$ and $p(\mathbf{z}|\mathbf{x})$:

$$\begin{align} D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)&= \mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg [ \log\frac{ q_\boldsymbol{\phi}({\mathbf{z}}) }{ p(\mathbf{z}|\mathbf{x}) }\bigg ] \\ &=\mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg [ \log\frac{ q_\boldsymbol{\phi}({\mathbf{z}})p_{\boldsymbol\theta}(\mathbf{x}) }{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }\bigg] \\ &=\mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg [ \log\frac{ q_\boldsymbol{\phi}({\mathbf{z}}) }{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }\bigg] + \mathbb{E}_{q_\boldsymbol{\phi}(\mathbf{z})} \log p_{\boldsymbol\theta}{(\mathbf{x})} \\ &=\mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg[ \log\frac{ q_\boldsymbol{\phi}({\mathbf{z}}) }{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }\bigg]+\log p_{\boldsymbol\theta}(\mathbf{x}) \\ \end{align}$$

We have used the equation:

$$\begin{align} \mathbb{E}_{q_{\boldsymbol{\phi}}{(\mathbf{z})}}\big [\log p_{\boldsymbol\theta}(\mathbf{x}) \big]&=\int q_{\boldsymbol{\phi}}(\mathbf{z}) \log p_{\boldsymbol\theta}(\mathbf{x})\,\mathrm{d}\mathbf{z} \\ &=\log p_{\boldsymbol\theta}(\mathbf{x}) \end{align}$$

Finally we can write:

$$\underbrace{ \log p_{\boldsymbol\theta}(\mathbf{x}) }_{\text{evidence}} = D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big) + \underbrace{ \mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg[ \log\frac{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }{ q_\boldsymbol{\phi}({\mathbf{z}}) }\bigg] }_{\text{ELBO}}$$

We should note than the set of $\{ \boldsymbol\theta,\boldsymbol\phi \}$ are the parameters we want to estimate . As we see the evidence is just a function of $\boldsymbol\theta$ so minimizing $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)$ with respect to $\boldsymbol\phi$ is equal to maximizing the ELBO with respect to this parameter. Also maximizing the ELBO with respect to $\boldsymbol\theta$ is equal to maximizing the likelihood. So instead of dealing with $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)$ which is intractable, we use the ELBO as our objective function.

Why did we start with $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)$?

In variational inference we are approximating an intractable distribution with a tractable one and we want to minimize their divergence (which is different from distance). KL divergence has some important properties:

1- $D_{\mathrm{KL}}(P\|Q)\geq 0 \quad \forall P,Q$

2- $D_{\mathrm{KL}}(P\|Q)=0 \quad$ if and only if $P=Q$

So based on these two conditions we see that both $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)$ and $D_{\mathrm{KL}}\big(p(\mathbf{z}|\mathbf{x})\| q_{\boldsymbol\phi}(\mathbf{z}) \big)$ could be our objective functions to make $p(\mathbf{z}|\mathbf{x})$ and $q_{\boldsymbol\phi}(\mathbf{z})$ as similar as possible but the problem with $D_{\mathrm{KL}}\big(p(\mathbf{z}|\mathbf{x})\| q_{\boldsymbol\phi}(\mathbf{z}) \big)$ is the intractable part:

$$D_{\mathrm{KL}}\big(p(\mathbf{z}|\mathbf{x})\| q_{\boldsymbol\phi}(\mathbf{z}) \big)= \int_{\mathbf{z}}{ \underbrace{ \dfrac{p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z})}{p_{\boldsymbol\theta}(\mathbf{x})} } _{f(p)} } \log{ \big( \underbrace{ \dfrac{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }{q_{\boldsymbol\phi}(\mathbf{z})p_{\boldsymbol\theta}(\mathbf{x})}} _{g(p,q)} \big) } \, \mathrm{d}{\mathbf{z}}$$

We should look for a way to separate tractable and intractable parts from $p(\mathbf{z}|\mathbf{x};\boldsymbol{\theta})$ and since both $f(p)$ and $g(p,q)$ include $p_{\boldsymbol\theta}(\mathbf{x})$, it’s not possible to derive tractable parts from the integral but as we showed in $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p(\mathbf{z}|\mathbf{x})\big)$ the intractable part ($p_{\boldsymbol\theta}(x)$) is just inside the $\log$ function which leads to ELBO.

What does ELBO mean?

By looking at the formula derived for the ELBO, we see:

$$\begin{align} \mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})}\bigg[ \log\frac{ p_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})p_{\boldsymbol\theta}(\mathbf{z}) }{ q_\boldsymbol{\phi}({\mathbf{z}}) }\bigg]= \mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})} {\log p_{\boldsymbol\theta}(\mathbf{x}|\mathbf{z})} - D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p_{\boldsymbol\theta}(\mathbf{z})\big) \end{align}$$

The ELBO shows that when we are approximating the posterior with $q_{\boldsymbol\phi}(\mathbf{z})$, first we have some prior information about $p_{\theta}(\mathbf{z})$ and it makes sense to minimize $D_{\mathrm{KL}}\big(q_{\boldsymbol\phi}(\mathbf{z})\|p_{\boldsymbol\theta}(\mathbf{z})\big)$. Also we have observed the data samples which we want to reconstruct and make them as probable as possible. So we should maximize $\mathbb{E}_{q_\boldsymbol{\phi}({\mathbf{z}})} {\log p_{\boldsymbol\theta}(\mathbf{x}|\mathbf{z})}$. In other words, before observing the data we had some information and now after observing them we have further information about the model and our approximation for the posterior should make a balance between them.

Refrences:

1-Autoencoding Variational Bayes

2-Variational Inference: A Review for Statisticians